


Next: Solver Submission
Up: Rules and submissions
Previous: Competition steps
The following benchmarks were submitted to Industrial
category:
- bart, homer
- from Fadi Aloul. Represent FPGA Switch-Box
problems, all instances should imply a lot of symmetries, as it is
described in [FAS02]. Bart instances are all satisfiable,
Homer instances are unsatisfiable.
- cmpadd
- from Armin Biere. These benchmarks encode the problem
of comparing the output of a carry ripple adder with the output of a
fast propagate and generate adder. They are all unsatisfiable.
- dinphil
- from Armin Biere. These benchmarks are generated from
bounded model checking from the well known dining philosophers
example. The instances have the generic name 'dp i t k cnf',
where 'i' is the number of philosophers, 'k' is the model
checking bound and 't' is 'u' for unsatisfiable or ' s' for satisfiable. The model for 'i' philosophers may reach
a bug not faster than in 'i' steps.
- cache, comb, f2clk, fifo8, ip, w08, w10
- from Emmanuel
Dellacherie (TNI-Valiosys, http://www.tni-valiosys.com/, France). All
these problems represent 18 industrial model-checking examples and 3
combinational equivalence examples.
- bmc1
- from Eugene Goldberg. Bounded Model Checking (BMC)
examples (76 CNFs, 30% of them are unsatisfiable ) encoding formal
verification of the open-source Sun PicoJava II (TM)
microprocessor. These CNFs were generated by Ken Mcmillan (Cadence
Berkeley Labs). The complete description of the benchmarks is given
at http://www-cad.eecs.berkeley.edu/~kenmcmil/satbench.html.
- bmc2
- from Eugene Goldberg, suggested by Ken Mcmillan (Cadence
Berkeley Labs). This small set of 6 BMC instances encodes testing
whether a sequential N-bit counter (file cntN.cnf) can reach a
final state from an initial state in
 cycles. In the
initial state all the bits of the counter are set to 0 and, in the
final state, all the bits of the counter are set to 1. All CNFs are
satisfiable.
cycles. In the
initial state all the bits of the counter are set to 0 and, in the
final state, all the bits of the counter are set to 1. All CNFs are
satisfiable.
- fpga_routing
- from Eugene Goldberg and Gi-Joon Nam (32 CNFs
submitted by E. Goldberg and 6 by G.-J. Nam separately, but all
instances were generated by G.-J. Nam). These Boolean SAT problems
are constructed by reducing FPGA (Field Programmable Gate Array)
detailed routing problems into Boolean SAT. More information on
transforming FPGA routing problems into SAT, are available at
http://andante.eecs.umich.edu/sdr/index.html.
- rand_net
- from Eugene Goldberg. This is a set of miter
CNFs (all unsatisfiable) produced from randomly generated
circuits. To produce a miter, a random circuit is generated
first. This circuit is specified by the number of primary input
variables (N), the number of levels in the circuit (M)
and the "length" (K) of wires connecting gates of the circuit
(K=1 means that the output of a gate may be connected only to
the input of a gate of the next level). A circuit consists of AND
and OR gates and does not contain inverters. So any circuit
implements a monotone function (by adding inverters to a randomly
generated circuit one can make it very redundant). Circuits are
"rectangular", i.e. the number of primary inputs, the number of
gates of m-th level, and the number of primary outputs are all equal
to N. Now, to check if a circuit is equivalent to itself, a
miter is formed. This class of benchmarks allow one to vary the
"topology" of the circuit by changing the "length" of wires. Each
instance is named rand_netN_M_K.miter.cnf where N,
M and K are the values of parameters described above.
- mediator
- from Steven Prestwich. The encoded problem (described
in [Pre02a]) is to construct a query plan to supply
attributes in a mediator system (e.g. an online bookstore). These
problems combine set covering with plan feasibility and involve
chains of reasoning that should make them hard for pure local
search. Symmetry breaking constraints were not added, in order to
make the problems harder for systematic backtrack search. A file
medN.cnf contains a problem with shortest known plan length
N.
- IBM
- from Emmanuel Zarpas (IBM). Bounded Model Checking for real
hardware formal verification. Benchmarks are partitioned by
difficulty in {Easy, Medium, Hard} by the submitter.
The following benchmarks were submitted to Handmade category:
- lisa
- from Fadi Aloul. Those instances represent integer
factorization problems. They are all satisfiable (see
[FAS02]). Note that other factorization problems (given as
generators) were submitted (described below).
- matrix, polynomial
- from Chu-Min Li (with Bernard Jurkowiak and
Paul W. Purdom). Those instances encode respectively the
multiplication of two
 matrices using
matrices using  products, and
the multiplication of two polynomials of degree-bound
products, and
the multiplication of two polynomials of degree-bound  using
using  products. Both problems should involve a lot of symmetries (see
[CMLP02]).
products. Both problems should involve a lot of symmetries (see
[CMLP02]).
- urquhart
- from Chu-Min Li (with Sebastien Cantarell and Bernard
Jurkowiak) [Li00] and independently from Laurent Simon
[CS00]. All instances are unsatisfiable and proved very
hard for all DLL and DP approaches (hard for all resolution-based
procedures, in general [Urq87]). Chu-Min Li benchmarks are
3-SAT encoding of Urquhart problems and Laurent Simon are non
reduced encoding (clauses can be long).
- hanoi
- from Eugene Goldberg (but generated by Henry
Kautz). These instances represent the classical problem of the
Towers of Hanoi, hand-encoded axioms around 1993 (similar to the
ones used in [JT96], but larger instances available).
- graphcolor

- from Dan Pehoushek. Random regular graph coloring
problems. Above some number of vertices, most of them should be
colorable.
- ezfact
- from Dan Pehoushek. SAT encoding of factorization
circuits.
- glassy-sat-sel
- from Federico Ricci-Tersenghi. Selected
instances (by the submitter) of medium hardness from the glassy-sat
generator (see below).
- gridmnbench
- from Allen Van Gelder. Encode (negated)
propositional theorem about a (non realistic) fault-tolerant circuit
family.
- checkerinterchange
- from Allen Van Gelder (with Fumiaki
Okushi). Planning problem to solve checker interchange problem within
deadline.
- ropebench
- from Allen Van Gelder. A linear family of graph
coloring problems (sequence of unsatisfiable formulas in 3-CNF).
The formula length is
linear in the number of variables (namely,
 ).
).
- qgbench
- from Hantao Zhang. Small instances of quasigroups with
constraints 0-7.
- sha
- from Lintao Zhang and Sharad Malik. CNF encoding of secure
hashing problems.
- xor-chains
- (among them, the smallest unsolved unsatisfiable
instance with 106 variables, 282 clauses and 844 literals), from
Lintao Zhang and Sharad Malik. This encodes verification problems of
2 xor chains.
- satex-challenges
- from Laurent Simon. Selection of
(heterogenous) unsolved instances from SAT-Ex [SC01].
- pyhala
- from Tuomo Pyhàlà. Submitted as a
generator. Depending on arguments, it can generate a SAT encoding of
factoring of primes (unsat instances) or products of two primes (sat
instances). The benchmarks encode multiplication circuits, with
predefined output. Two circuits are available (braun or
adder-tree multipliers).
The benchmarks of Random category were submitted as
generators (except for plainoldcnf and twentyvars):
- 3sat
- from the organizers. This generator produces uniform 3-CNF formulas.
Checks are performed to prevent duplicate or opposite literals in
clauses. In addition, no duplicate clause are created.
- glassy-sat
- from Federico Ricci-Tersenghi (with W. Barthel,
A.K. Hartmann, M. Leone, M. Weigt, and R. Zecchina). Generator of
hard and solvable 3-SAT instances, corresponding to a glassy model in
statistical physics. A description is available as a preprint at
http://xxx.lanl.gov/abs/cond-mat/0111153.
- okrandgen
- from Oliver Kullman [Kul02c,Kul02a],
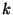 -CNF uniform random generator,
based on encryption functions to ensure strong and
reliable random formulae. Detailed description and sources
available at
http://cs-svr1.swan.ac.uk/~csoliver/OKgenerator.html.
-CNF uniform random generator,
based on encryption functions to ensure strong and
reliable random formulae. Detailed description and sources
available at
http://cs-svr1.swan.ac.uk/~csoliver/OKgenerator.html.
- hgen2
- from Edward A. Hirsch
(available from http://logic.pdmi.ras.ru/~hirsch/benchmarks/hgen2.html).
An instance generated by this generator (3-CNF, 500 variables, 1750
clauses, 5250 literals, seed 1216665065)
was the smallest satisfiable benchmark
that remained unsolved during the competition.
Description: First a satisfying assignment is chosen;
then clauses (
 of them for
of them for  variables) are generated
one by one. A literal cannot be put into a clause if
variables) are generated
one by one. A literal cannot be put into a clause if
- There is a less frequent literal.
- The corresponding variable already appears in the current clause.
- A variable dependent on it (i.e., occurred together in another clause)
already appears in the current clause.
- A variable dependent on a dependent variable
already appears in the current clause.
- The opposite literal is not satisfying and occurs not more frequently
(except for the case that choosing a satisfying literal
is our last chance to satisfy this clause).
If the generation process fails (no literal can be chosen), it is restarted
from the beginning.
- hgen1
- from Edward A. Hirsch. Similar to hgen2 except for condition 5.
- hgen3
- from Edward A. Hirsch. Similar to hgen1, but formulas are not
required to be satisfiable.
- hgen4
- from Edward A. Hirsch. Similar to hgen2, but formulas are in
4-CNF, with
 clauses.
Also condition 4 is not applied.
clauses.
Also condition 4 is not applied.
- hgen5
- from Edward A. Hirsch. Similar to hgen2, but formulas are a mix
of 3-CNF (
 clauses) and 4-CNF (
clauses) and 4-CNF ( clauses).
clauses).
- g3
- from Mitsuo Motoki. Generates positive instances at random.
These instances have only one solution with high
probability. Benchmarks were discarded because of a bug in the
generator.
- plainoldcnf
- from Dan Pehoushek. Selection of regular random
5-CNF.
- twentyvars
- from Dan Pehoushek. Small instances (in terms of
their number of variables) of
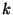 -CNF, with
-CNF, with
 .
.



Next: Solver Submission
Up: Rules and submissions
Previous: Competition steps
LE BERRE Daniel
2002-09-16